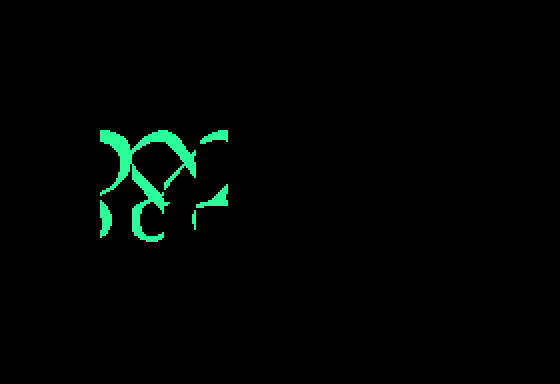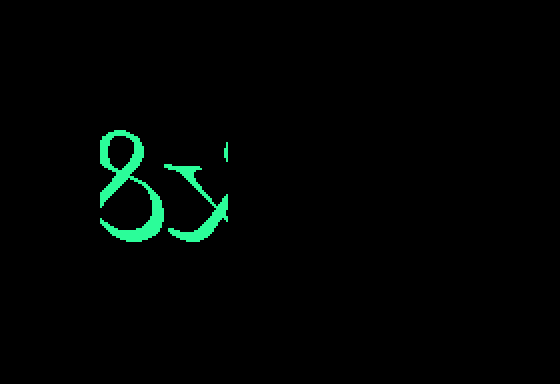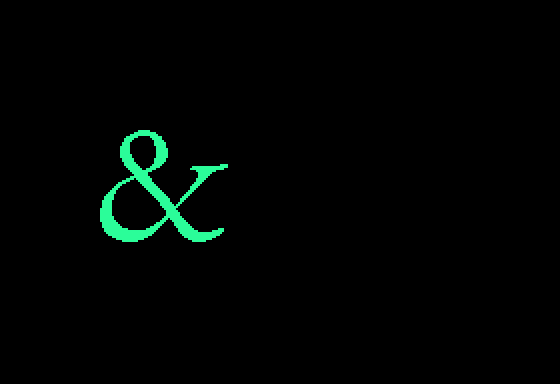[Also known as DRAWBLOCK in Apple Pascal (Apple II).]
DRAWBL can be used to send an array to the graphics screen. However, this function is not well documented, and hard to use. After a time, I did manage to make it work, but I suspect it would be much easier, although maybe somewhat slower, to call SCREEN and FILLSC as needed.
Let’s say you want to transfer a small image to the screen, say an ampersand that looks like this:
First step is to convert this bitmap data into a format that DRAWBL will accept, that is, an integer array. There are probably many ways to do this, but the simplest and most ‘visual’ way I could think of was to make an ASCII text file of ‘0’ and ‘1’ characters, and then convert those fake bits to real words.
ppmtoascii looks good on a terminal, but unfortunately is scaled 2:1 vertically, which would result in a ‘squished’ image.
ppmtoterm is a better choice, but its output is full of control codes which will be unsuitable. You can use sed (or gsed) to strip out the codes, leaving a ‘0’ for an ‘off’ pixel and a ‘1’ for an ‘on’ pixel:
$ convert ampersand2.png ampersand2.ppm $ ppmtoterm ampersand2.ppm | gsed -e 's,\x1b\[1m\x1b\[37m\x1b\[40m\xb1,0,g' -e 's,\x1b\[0m\x1b\[30m\x1b\[40m\xb1,1,g' -e 's,\x1b\[0m$,,' 0000000000000000000111111000000000000000000000000000000000000000 0000000000000000011111111111000000000000000000000000000000000000 0000000000000001111111111111100000000000000000000000000000000000 0000000000000111111000000111111000000000000000000000000000000000 0000000000001111100000000011111000000000000000000000000000000000 0000000000001111000000000001111100000000000000000000000000000000 0000000000011110000000000001111110000000000000000000000000000000 0000000000011110000000000001111110000000000000000000000000000000 0000000000111110000000000000111110000000000000000000000000000000 0000000000111110000000000000111111000000000000000000000000000000 0000000000111110000000000000111111000000000000000000000000000000 0000000000111110000000000000111111000000000000000000000000000000 0000000000111111000000000000111111000000000000000000000000000000 0000000000111111000000000000111111000000000000000000000000000000 0000000000011111100000000001111110000000000000000000000000000000 0000000000011111100000000001111110000000000000000000000000000000 0000000000001111110000000001111100000000000000000000000000000000 0000000000001111111000000011111000000000000000000000000000001111 0000000000000111111100000111110000000000000000111111111111111111 0000000000000011111110011111000000000000000001111111111111111100 0000000000000001111111111100000000000000000000001111111111000000 0000000000000000111111110000000000000000000000000111111100000000 0000000000000000011111110000000000000000000000000111111000000000 0000000000000001111111111000000000000000000000000111110000000000 0000000000000111101111111100000000000000000000001111100000000000 0000000000011110000111111100000000000000000000001111000000000000 0000000001111000000011111110000000000000000000011110000000000000 0000000011100000000001111111000000000000000000111100000000000000 0000000111000000000000111111100000000000000001111000000000000000 0000001110000000000000011111110000000000000001110000000000000000 0000011100000000000000001111111000000000000011100000000000000000 0000111100000000000000000111111100000000000111000000000000000000 0001111000000000000000000011111110000000001110000000000000000000 0011111000000000000000000001111111000000011100000000000000000000 0011111000000000000000000000111111100000111000000000000000000000 0111110000000000000000000000011111100000110000000000000000000000 0111110000000000000000000000001111110001100000000000000000000000 0111110000000000000000000000001111111011000000000000000000000000 0111110000000000000000000000000111111110000000000000000000000000 1111110000000000000000000000000011111100000000000000000000000000 1111110000000000000000000000000001111110000000000000000000000000 1111110000000000000000000000000001111111000000000000000000000000 1111110000000000000000000000000001111111000000000000000000000000 1111111000000000000000000000000011111111100000000000000000000000 1111111000000000000000000000000111011111110000000000000000000000 1111111100000000000000000000001110001111111000000000000000000000 0111111110000000000000000000111100000111111100000000000000000000 0111111111000000000000000001111000000111111110000000000000000000 0111111111100000000000000111110000000011111111000000000000000000 0011111111111100000000011111100000000001111111100000000000011100 0011111111111111111111111111000000000001111111111000000011111100 0001111111111111111111111110000000000000111111111111111111111000 0000111111111111111111111100000000000000011111111111111111110000 0000001111111111111111110000000000000000001111111111111111000000 0000000011111111111111000000000000000000000011111111111100000000 0000000000011111111000000000000000000000000000111111100000000000
In Apple FORTRAN, the INTEGER data type is 16 bits, so my idea was to convert each row (64 px) into 4 INTEGERs. I wrote a simple bit of C to read the digits and output four int16_t integers. Let’s look at the first three rows generated:
$ ./bitstowords ampersand2.txt | head -3 0000000000000000000111111000000000000000000000000000000000000000 0 8064 0 0 0000000000000000011111111111000000000000000000000000000000000000 0 32752 0 0 0000000000000001111111111111100000000000000000000000000000000000 1 -8 0 0
The second word in all three rows is useful for validation, as it clearly shows a negative number working (1 in the most significant bit), as well as a number close to its upper limit (32752). Here’s how that breaks down:
word 1 word 2 word 3 word 4 row 1 0000000000000000
= 00001111110000000
= 80640000000000000000
= 00000000000000000
= 0row 2 0000000000000000
= 00111111111110000
= 327520000000000000000
= 00000000000000000
= 0row 3 0000000000000001
= 11111111111111000
= −80000000000000000
= 00000000000000000
= 0
With this, it should be possible to use DATA statements to fill an array, eg:
INTEGER A(224)
DATA A /0,8064,0,0,0,32752,0,0,1,-8,0,0, .../(And deliberately using a one-dimensional array to avoid issues with row vs column ordering.)
However, I ran into two problems rather quickly:
- The number of integers in the array (4×56 = 224) meant that the DATA statement exceeded the maximum line length of 660 characters, that is, more than 9 continuation lines. So this means the graphic had to be broken into two arrays.
- While −32768 is a valid number (ie, with the range of an INTEGER), it isn’t accepted as such by the FORTRAN compiler. Probably this is a bug; I imagine the check is something like ±32767 rather than the true range of −32768 through +32767. The ‘fix’ here is to use a different number (−32767, in my case) and manually fix it up. This is very kludgy and not something I expected to have to do.
Making changes to accommodate those issues, I got the following bit of FORTRAN:
$USES APPLESTUFF
$USES TURTLEGRAPHICS
$XREF
PROGRAM AMPERS
INTEGER A(112),B(112)
DATA A /0,8064,0,0,0,32752,0,0,1,-8,0,0,7,-8066,0,0,15,-32706,0,0,
+15,31,0,0,30,31,-32767,0,30,31,-32767,0,62,15,-32767,0,62,15,
+-16384,0,62,15,-16384,0,62,15,-16384,0,63,15,-16384,0,63,15,
+-16384,0,31,-32737,-32767,0,31,-32737,-32767,0,15,-16353,0,0,15,
+-8130,0,15,7,-3972,3,-1,3,-1552,7,-4,1,-64,0,-64,0,-256,0,32512,0,
+32512,0,32256,1,-128,0,31744,7,-16448,0,-2048,30,8128,0,-4096,120,
+4064,1,-8192,224,2032,3,-16384/
DATA B /448,1016,7,-32767,896,508,7,0,1792,254,14,0,3840,127,28,0,
+7680,63,-32712,0,15872,31,-16272,0,15872,15,-7968,0,31744,7,-8000,
+0,31744,3,-3712,0,31744,3,-1280,0,31744,1,-512,0,-1024,0,-1024,0,
+-1024,0,32256,0,-1024,0,32512,0,-1024,0,32512,0,-512,0,-128,0,
+-512,1,-8256,0,-256,3,-28704,0,32640,15,2032,0,32704,30,2040,0,
+32736,124,1020,0,16380,504,510,28,16383,-16,511,-32516,8191,-32,
+255,-8,4095,-64,127,-16,1023,-256,63,-64,255,-1024,15,-256,31,
+-8192,3,-2048/
DO 10 I=1,112
IF(A(I).EQ.-32767)THEN
A(I)=A(I)-1
ENDIF
IF(B(I).EQ.-32767)THEN
B(I)=B(I)-1
ENDIF
10 CONTINUE
CALL INITTU
CALL DRAWBL (A, 8, 0, 0, 64, 28, 50, 71, 10)
CALL DRAWBL (B, 8, 0, 0, 64, 28, 50, 99, 10)
READ(*,30)
30 FORMAT(A)
ENDWhich produced the following mess:
Although at first glance this might look discouraging, anyone that has tried DRAWBL will know that this is actually a very promising result. Actually all of the code is correct; only the data needs some work.
Before getting into the data fixing, let’s break down the arguments to DRAWBL to see how it works:
DRAWBL arguments
Argument Explanation source An array to be copied to the screen. This could be a one- or two-dimensional array (at least theoretically; I haven’t tested it) of INTEGER type (not BOOLEAN as the documentation says!). I think CHARACTER type should also be possible. In my case, the source array A is for the top half, and B for the lower half. rowsize The number of bytes per row. In the above case, a row is 64 px wide, which would require 8 bytes to store. (Not sure what happens when your row length is not an exact multiple of 8; presumably some of the bits are thrown away?) xskip How many X (ie, horizontal) bits to “skip over”; mentally, I imagine this to be if you wanted to draw a subset of a particular array (combined with yskip, width, and height). 0 in this case, as I intend to use the entire array. yskip How many Y (ie, vertical) bits to “skip over” (see above). width How many dots width of the array will be used. height How many dots height of the array will be used. xscreen The starting X point on the screen [0,279], drawing from left to right. I just picked 50 as a nice number; it has no real significance, except that (50+64) < 279. yscreen The starting Y point on the screen [0,191], drawing from bottom to top (maybe counterintuitively). 71 was chosen arbitrarily, and 99 is 71 + 28, so that A and B are adjacent. mode I won’t go into all of the 16 modes here, but there are various options for how to copy the array, including some Boolean combinations with existing screen content, not even copying the array at all (!), etc. 10 is the most sensible, as it just copies the array exactly as it is, completely overwriting the screen area.
Fixing the data
The first ‘obvious’ problem is that the ampersand is upside-down. I should’ve remembered this, as the screen draws ‘upwards’ from bottom to top, but forgot. That’s easy enough to fix: just reverse the line order from the ascii-bits-to-words converter:
$ ./bitstowords ampersand2.txt | cat -n | sort -rn | awk '{ printf "%s\t%s\t%s\t%s\t%s\n", $2, $3, $4, $5, $6 }'
0000000000011111111000000000000000000000000000111111100000000000 31 -8192 3 -2048
0000000011111111111111000000000000000000000011111111111100000000 255 -1024 15 -256
0000001111111111111111110000000000000000001111111111111111000000 1023 -256 63 -64
[...]The second problem seems to have something to do with byte ordering. The 6502 is little endian, so it’s unsurprising that just stuffing the bytes in big-endian order didn’t give the right result. Maybe swapping words 1/2 and 3/4 would help:
$ ./bitstowords ampersand2.txt | cat -n | sort -rn | awk '{ print $4, $3, $6, $5 }'
-8192 31 -2048 3
-1024 255 -256 15
-256 1023 -64 63
[...]That gives DATA statements:
DATA A /-8192,31,-2048,3,-1024,255,-256,15,-256,1023,-64,63,-64,
+4095,-16,127,-32,8191,-8,255,-16,16383,-32516,511,504,16380,28,
+510,124,32736,0,1020,30,32704,0,2040,15,32640,0,2032,3,-256,0,
+-28704,1,-512,0,-8256,0,-512,0,-128,0,-1024,0,32512,0,-1024,0,
+32512,0,-1024,0,32256,0,-1024,0,-1024,1,31744,0,-512,3,31744,0,
+-1280,3,31744,0,-3712,7,31744,0,-8000,15,15872,0,-7968,31,15872,0,
+-16272,63,7680,0,-32712,127,3840,0,28,254,1792,0,14,508,896,0,7,
+1016,448,-32767,7/
DATA B /2032,224,-16384,3,4064,120,-8192,1,8128,30,-4096,0,-16448,
+7,-2048,0,-128,1,31744,0,32512,0,32256,0,-256,0,32512,0,-64,1,-64,
+0,-1552,3,-4,7,-3972,7,-1,3,-8130,15,15,0,-16353,15,0,0,-32737,31,
+0,-32767,-32737,31,0,-32767,15,63,0,-16384,15,63,0,-16384,15,62,0,
+-16384,15,62,0,-16384,15,62,0,-16384,15,62,0,-32767,31,30,0,
+-32767,31,30,0,-32767,31,15,0,0,-32706,15,0,0,-8066,7,0,0,-8,1,0,
+0,32752,0,0,0,8064,0,0,0/And the not-quite-right result of:
Interestingly, even with words ordered 2, 1, 4, 3, the output is still wrong; it would have to be 4, 3, 2, 1. But the above image also makes something else quite clear: the image itself is entirely reversed (ie, the bits themselves are completely backwards). Fortunately the rev command can do that part:
$ rev ampersand2.txt > ampersand3.txt ; ./bitstowords ampersand3.txt 0000000000000000000000000000000000000001111110000000000000000000 0 0 504 0 0000000000000000000000000000000000001111111111100000000000000000 0 0 4094 0 0000000000000000000000000000000000011111111111111000000000000000 0 0 8191 -32768 0000000000000000000000000000000001111110000001111110000000000000 0 0 32263 -8192 0000000000000000000000000000000001111100000000011111000000000000 0 0 31745 -4096 0000000000000000000000000000000011111000000000001111000000000000 0 0 -2048 -4096 0000000000000000000000000000000111111000000000000111100000000000 0 1 -2048 30720 0000000000000000000000000000000111111000000000000111100000000000 0 1 -2048 30720 0000000000000000000000000000000111110000000000000111110000000000 0 1 -4096 31744 0000000000000000000000000000001111110000000000000111110000000000 0 3 -4096 31744 0000000000000000000000000000001111110000000000000111110000000000 0 3 -4096 31744 0000000000000000000000000000001111110000000000000111110000000000 0 3 -4096 31744 0000000000000000000000000000001111110000000000001111110000000000 0 3 -4096 -1024 0000000000000000000000000000001111110000000000001111110000000000 0 3 -4096 -1024 0000000000000000000000000000000111111000000000011111100000000000 0 1 -2047 -2048 0000000000000000000000000000000111111000000000011111100000000000 0 1 -2047 -2048 0000000000000000000000000000000011111000000000111111000000000000 0 0 -2045 -4096 1111000000000000000000000000000001111100000001111111000000000000 -4096 0 31751 -4096 1111111111111111110000000000000000111110000011111110000000000000 -1 -16384 15887 -8192 0011111111111111111000000000000000001111100111111100000000000000 16383 -8192 3999 -16384 0000001111111111000000000000000000000011111111111000000000000000 1023 0 1023 -32768 0000000011111110000000000000000000000000111111110000000000000000 254 0 255 0 0000000001111110000000000000000000000000111111100000000000000000 126 0 254 0 0000000000111110000000000000000000000001111111111000000000000000 62 0 511 -32768 0000000000011111000000000000000000000011111111011110000000000000 31 0 1021 -8192 0000000000001111000000000000000000000011111110000111100000000000 15 0 1016 30720 0000000000000111100000000000000000000111111100000001111000000000 7 -32768 2032 7680 0000000000000011110000000000000000001111111000000000011100000000 3 -16384 4064 1792 0000000000000001111000000000000000011111110000000000001110000000 1 -8192 8128 896 0000000000000000111000000000000000111111100000000000000111000000 0 -8192 16256 448 0000000000000000011100000000000001111111000000000000000011100000 0 28672 32512 224 0000000000000000001110000000000011111110000000000000000011110000 0 14336 -512 240 0000000000000000000111000000000111111100000000000000000001111000 0 7169 -1024 120 0000000000000000000011100000001111111000000000000000000001111100 0 3587 -2048 124 0000000000000000000001110000011111110000000000000000000001111100 0 1799 -4096 124 0000000000000000000000110000011111100000000000000000000000111110 0 775 -8192 62 0000000000000000000000011000111111000000000000000000000000111110 0 399 -16384 62 0000000000000000000000001101111111000000000000000000000000111110 0 223 -16384 62 0000000000000000000000000111111110000000000000000000000000111110 0 127 -32768 62 0000000000000000000000000011111100000000000000000000000000111111 0 63 0 63 0000000000000000000000000111111000000000000000000000000000111111 0 126 0 63 0000000000000000000000001111111000000000000000000000000000111111 0 254 0 63 0000000000000000000000001111111000000000000000000000000000111111 0 254 0 63 0000000000000000000000011111111100000000000000000000000001111111 0 511 0 127 0000000000000000000000111111101110000000000000000000000001111111 0 1019 -32768 127 0000000000000000000001111111000111000000000000000000000011111111 0 2033 -16384 255 0000000000000000000011111110000011110000000000000000000111111110 0 4064 -4096 510 0000000000000000000111111110000001111000000000000000001111111110 0 8160 30720 1022 0000000000000000001111111100000000111110000000000000011111111110 0 16320 15872 2046 0011100000000000011111111000000000011111100000000011111111111100 14336 32640 8064 16380 0011111100000001111111111000000000001111111111111111111111111100 16129 -128 4095 -4 0001111111111111111111110000000000000111111111111111111111111000 8191 -256 2047 -8 0000111111111111111111100000000000000011111111111111111111110000 4095 -512 1023 -16 0000001111111111111111000000000000000000111111111111111111000000 1023 -1024 255 -64 0000000011111111111100000000000000000000001111111111111100000000 255 -4096 63 -256 0000000000011111110000000000000000000000000001111111100000000000 31 -16384 7 -2048
Combining all of the fixes together gives for the A half:
$ ./bitstowords ampersand3.txt | cat -n | sort -rn | awk '{ print $6,$5,$4,$3 }' | head -28 | tr '\n' ',' | tr ' ' ','
-2048,7,-16384,[...]And for the B half:
$ ./bitstowords ampersand3.txt | cat -n | sort -rn | awk '{ print $6,$5,$4,$3 }' | tail -28 | tr '\n' ',' | tr ' ' ','
1792,4064,-16384,[...]Which gives the combined DATA statements:
DATA A /-2048,7,-16384,31,-256,63,-4096,255,-64,255,-1024,1023,
+-16,1023,-512,4095,-8,2047,-256,8191,-4,4095,-128,16129,16380,
+8064,32640,14336,2046,15872,16320,0,1022,30720,8160,0,510,-4096,
+4064,0,255,-16384,2033,0,127,-32767,1019,0,127,0,511,0,63,0,254,0,
+63,0,254,0,63,0,126,0,63,0,63,0,62,-32767,127,0,62,-16384,223,0,
+62,-16384,399,0,62,-8192,775,0,124,-4096,1799,0,124,-2048,3587,0,
+120,-1024,7169,0,240,-512,14336,0,224,32512,28672,0,448,16256,
+-8192,0,896,8128,-8192,1/
DATA B /1792,4064,-16384,3,7680,2032,-32767,7,30720,1016,0,15,
+-8192,1021,0,31,-32767,511,0,62,0,254,0,126,0,255,0,254,-32767,
+1023,0,1023,-16384,3999,-8192,16383,-8192,15887,-16384,-1,-4096,
+31751,0,-4096,-4096,-2045,0,0,-2048,-2047,1,0,-2048,-2047,1,0,
+-1024,-4096,3,0,-1024,-4096,3,0,31744,-4096,3,0,31744,-4096,3,0,
+31744,-4096,3,0,31744,-4096,1,0,30720,-2048,1,0,30720,-2048,1,0,
+-4096,-2048,0,0,-4096,31745,0,0,-8192,32263,0,0,-32767,8191,0,0,0,
+4094,0,0,0,504,0,0/And – finally! – a successful image:
Knowing all this, a faster way to get here would be to apply a 180° rotation to the image first; then you only need to return the words in reverse order and you’re done:
$ convert ampersand2.ppm -rotate 180 ampersand4.ppm
$ ppmtoterm ampersand4.ppm | gsed -e 's,\x1b\[1m\x1b\[37m\x1b\[40m\xb1,0,g' -e 's,\x1b\[0m\x1b\[30m\x1b\[40m\xb1,1,g' -e 's,\x1b\[0m$,,' > ampersand4.txt
$ ./bitstowords ampersand4.txt | awk '{ print $5, $4, $3, $2 }' | tr '\n' ',' | tr ' ' ','
-2048,7,-16384,[...]